| ||||||
|
| |||||
|
Дистанционная школа
Занятие "Поиск путей в графе" 1 этап. Актуализация знаний. КРОССВОРД
2 этап. Лекция (повторение теоретического материала) Графические информационные модели
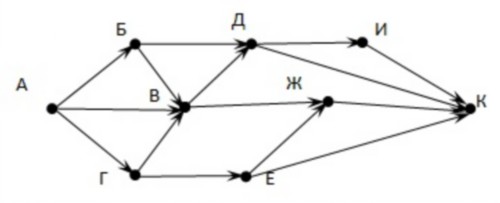
3 этап. Формирование новых знаний. Разбор задач типа В11 ГИА. Тема: Графы. Поиск путей Что нужно знать: · если в город R можно приехать только из городов X, Y, и Z, то число различных путей из города A в город R равно сумме числа различных путей проезда из A в X, из A в Y и из A в Z, то есть ПR=ПX+ПY+ПZ; где ПQ обозначает число путей из вершины A в некоторую вершину Q; · число путей конечно, если в графе нет циклов – замкнутых путей. Примеры заданий:Задача 1. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
Решение:
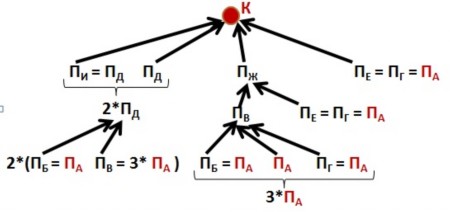
Пусть ПА – путь из города А. Соответственно, ПХ – путь из некого города Х. Идея метода: заменять пути ПХ на те, которые ближе к городу А (см. схему ниже). Начнем движение с конца маршрута (с города К), к которому ведут четыре пути: ПИ , ПД , ПЖ , ПЕ В город И есть только один путь – из города Д, поэтому заменяем путь ПИ на тот, который ближе к городу А, т.е. на ПД . Отметим: ПИ = ПД Также поступаем в направлении города Е: ПЕ = ПГ = ПА В город Ж ведут два пути: ПВ и ПЕ . Мы уже выполнили замену: ПЕ = ПГ = ПА В город В ведут три пути, для некоторых из которых уже возможна замена: Количество различных путей из города А равно 2*4*ПА + 3*ПА + ПА + ПА = 13
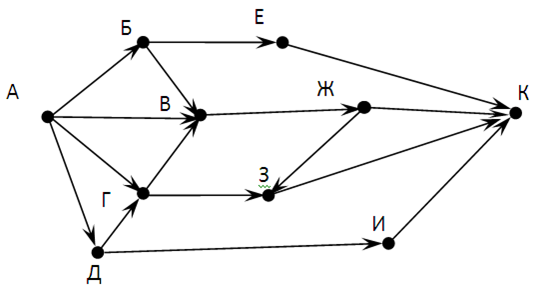
Ответ: 13 Задача 2. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?
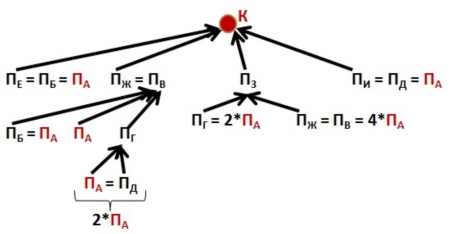
Решение: Пусть ПА – путь из города А. Соответственно, ПХ – путь из некого города Х. Идея метода: заменять пути ПХ на те, которые ближе к городу А (см. схему ниже). Начнем движение с конца маршрута (с города К), к которому ведут четыре пути: ПЕ , ПЖ , ПЗ , ПИ В город Е есть только один путь – из города Б, поэтому заменяем путь ПЕ на тот, который ближе к городу А, т.е. на ПБ . Отметим: ПЕ = ПБ . Следуя тому же правилу, делаем вывод: ПЕ = ПБ = ПА . По аналогии - в направлении города И: ПИ = ПД = ПА Также поступаем в направлении города Ж: ПЖ = ПВ В город В ведут три пути: ПБ , ПА , ПГ, причём ПБ = ПА , а ПГ =2*ПА В город З ведут два пути: ПГ и ПЖ, для каждого из которых уже можно выполнить замену: ПГ = 2*ПА и ПЖ= ПВ = 4*ПА. На схеме считаем пути ПА. Количество различных путей из города А равно:
Ответ: 12
4 этап. Физкультминутка для глаз
5 этап. ДОМАШНЕЕ ЗАДАНИЕ
6 этап. Тест | ||||||
|
| ||||||
| Сайт создан по технологии «Конструктор сайтов e-Publish» | ||||||